引言

ICNet是一个专注于实时语义分割的模型，这意味着它的运行速度更快，模型更小，参数量也更少。但是这些指标的提升难免会带来性能精度的下降，于是作者提出了一种级联式的网络架构帮助恢复图像边缘等细节信息。本文作者为Hengshuang Zhao, Xiaojuan Qi, Xiaoyong Shen, Jianping Shi, Jiaya Jia

原论文

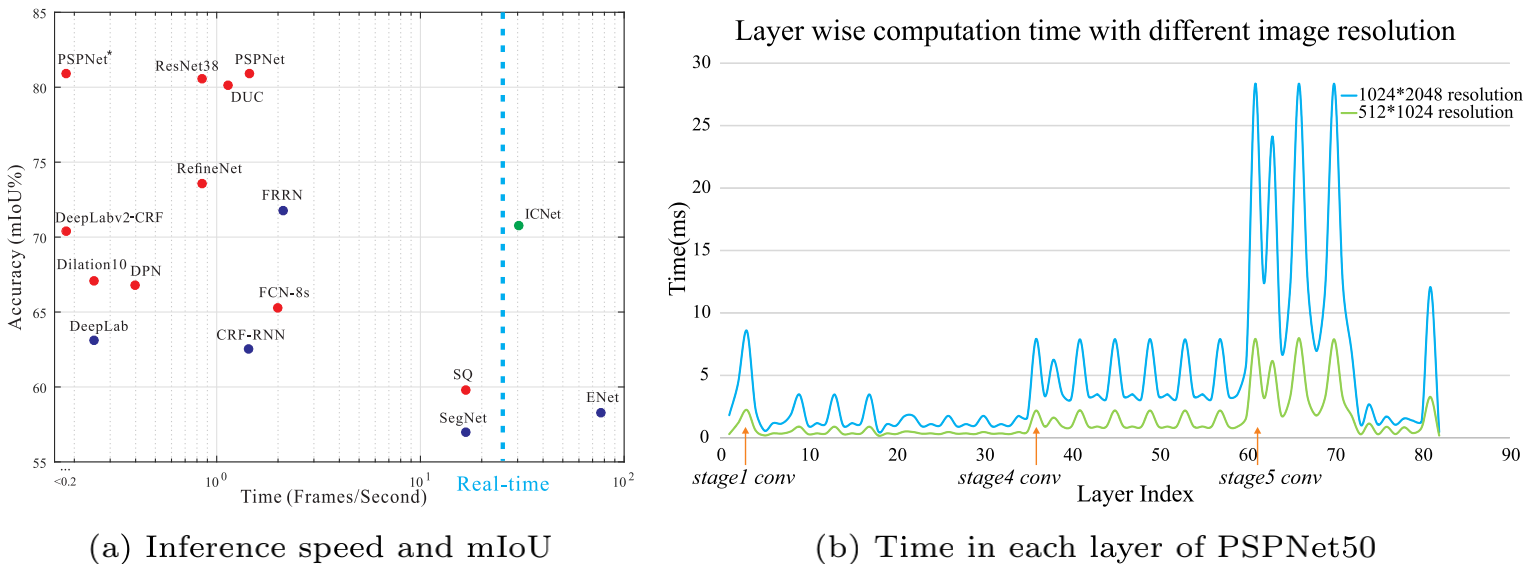
网络结构

速度分析

在卷积网络中，输入特征图V维度为$c\times h\times w$,经过卷及操作输出特征图U维度为$c^,\times h^, \times w^,$，其中c,h,w分别代表特征图的长，宽和通道数。卷积操作是通过一个维度为$c\times k \times k$的卷积核K实现V到U的映射的，其中$k\times k$就代表卷积核大小。所以卷积操作的操作数量为$c^,ck^2h^,w^,$。其中又因为$h^,=\frac{h}{s},w^,=\frac{w}{s}$，操作数量式子又可以变换为$c^,ck^2h\frac{w}{s^2}$。

由以上最终式子可以看出计算复杂度取决于特征度的分辨率(w,h)，输入特征图的通道数(c)和卷积核数量($c^,$)。

上图中(b)显示了PSPNet50处理两种不同分辨率图片的各层计算量，蓝色曲线代表的是处理分辨率为$1024\times2048$的图片，绿色曲线为$512\times1024$。可以发现对于分辨率大的图片在stage5计算量大幅增加。

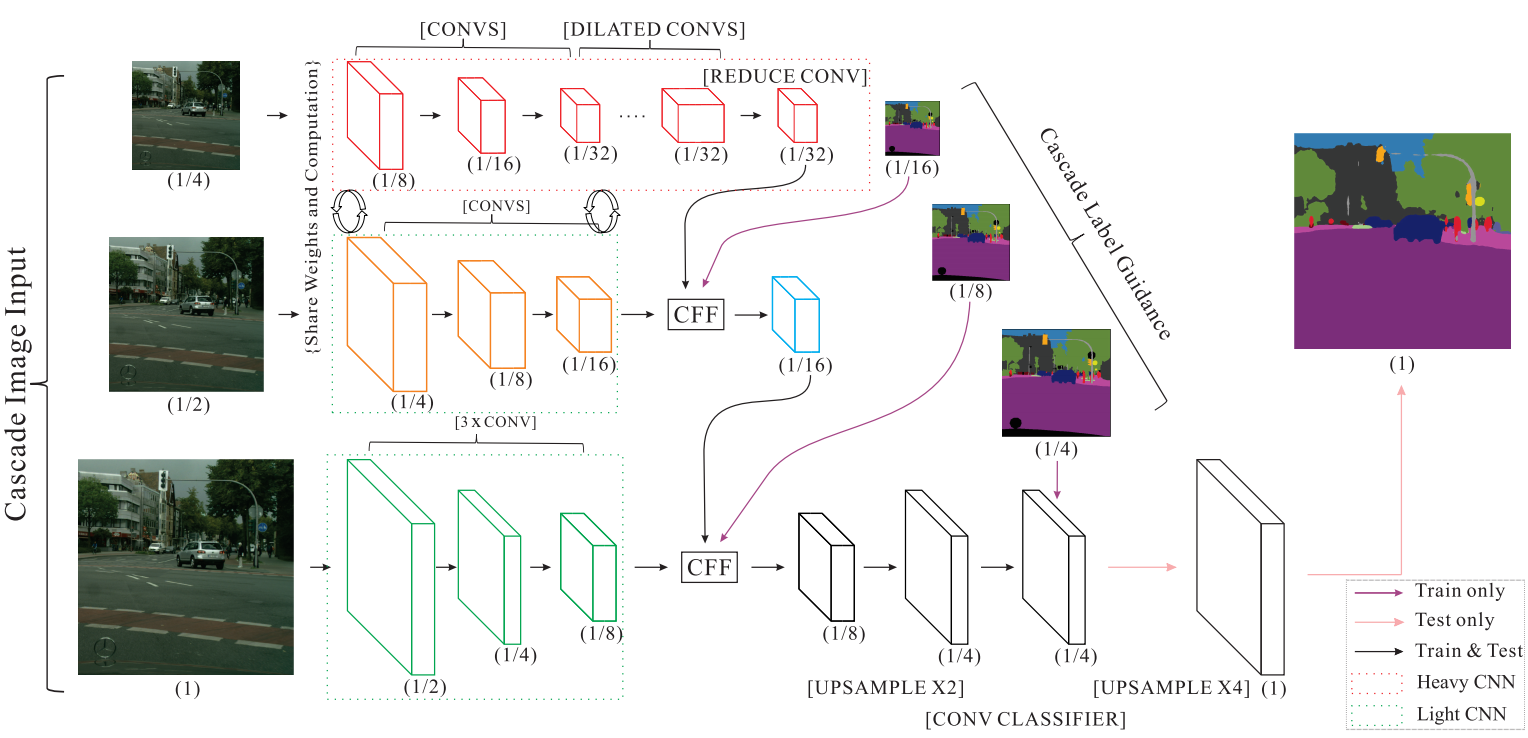
架构

想要在速度和准确度合适的取舍是很困难的，减少模型复杂度可以提高速度，但是却会使准确度大幅下降，而复杂的模型又十分耗时。作者没有单一的选取其中的任何一个，而是把两者结合提出了一种级联式的网络结构，即image cascade network，网络结构图如下:

它采用了三种不同分辨率的图，分别是原图，$\frac{1}{2}$原图大小的图片和$\frac{1}{4}$原图大小的图片作为输入。对原图使用传统大型语义分割网络是很消耗计算量的，所以作者使用传统分割网络对$\frac{1}{4}$的图片进行分割，由于图像分辨率小了很多，所以计算量是非常少的（由之前列举的PSPNet50处理不同分辨率图可看出）。具体来说是使用PSPNet对$\frac{1}{4}$图进行8倍下采样，就得到了原图大小$\frac{1}{32}$的特征图（如上图第一行所示）。为了获得更好的分割效果，使用原图和$\frac{1}{2}$图帮助恢复图像细节信息，$\frac{1}{2}$图仅仅进行8倍下采样就与之前的特征图进行CFF操作，原图也只经过一个非常简单的CNN网络进行8倍下采样然后与之前层级的融合特征图进行CFF操作再上采样恢复原图大小。

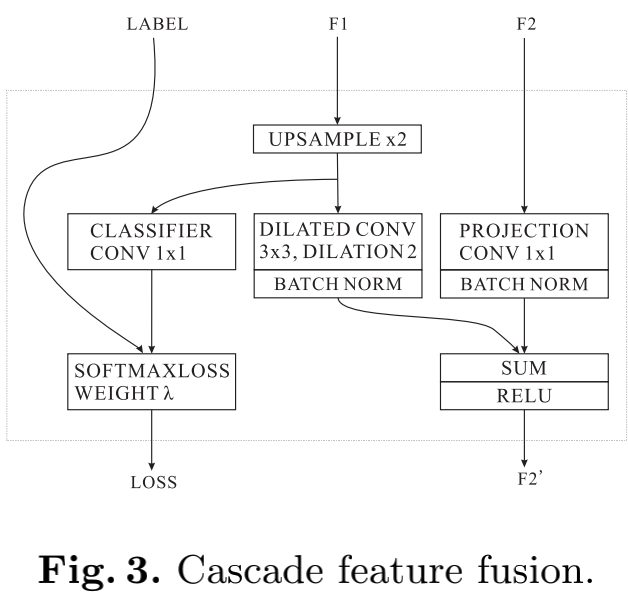
Cascade Feature Fusion(CFF)

模型图中的CFF模块是用来把低分辨率的图片与高分辨率图片融合的一个模块，同时还有带有输出辅助损失函数，具体图如下：

从图中可以看出该模块的F1输入即低分辨率的特征图，经过2倍上采样得到与高一级的特征图同样分辨率的大小，再经过一个空洞卷积与F2做相加。而F2即比F1高一级分辨率的特征图，它做一个简单的$1\times1$卷积投影映射与F1相加。

除此之外，CFF模块还附加了一个辅助的损失函数输出，将这些损失函数相加得到总损失函数再进行优化，可以使梯度优化更加平滑，并且有更强的学习能力。

最终的损失函数定义为:

$L = -\sum_{t=1}^T\lambda_t\frac{1}{y_tx_t}\sum_{y=1}^{y_t}\sum_{x=1}^{x_t}log\frac{e^{F_{n^{hat},y,x}^t}}{\sum_{n=1}^Ne^{F_{n,y,x}^t}}$

整个函数后半部分Wie标准的softmax损失函数，前面加了个对t从1到T的求和，t表示的就是有几个辅助损失函数，把它们带权相加就是最终的损失函数L，$\lambda_t$即为权重系数。

模型比较与分析

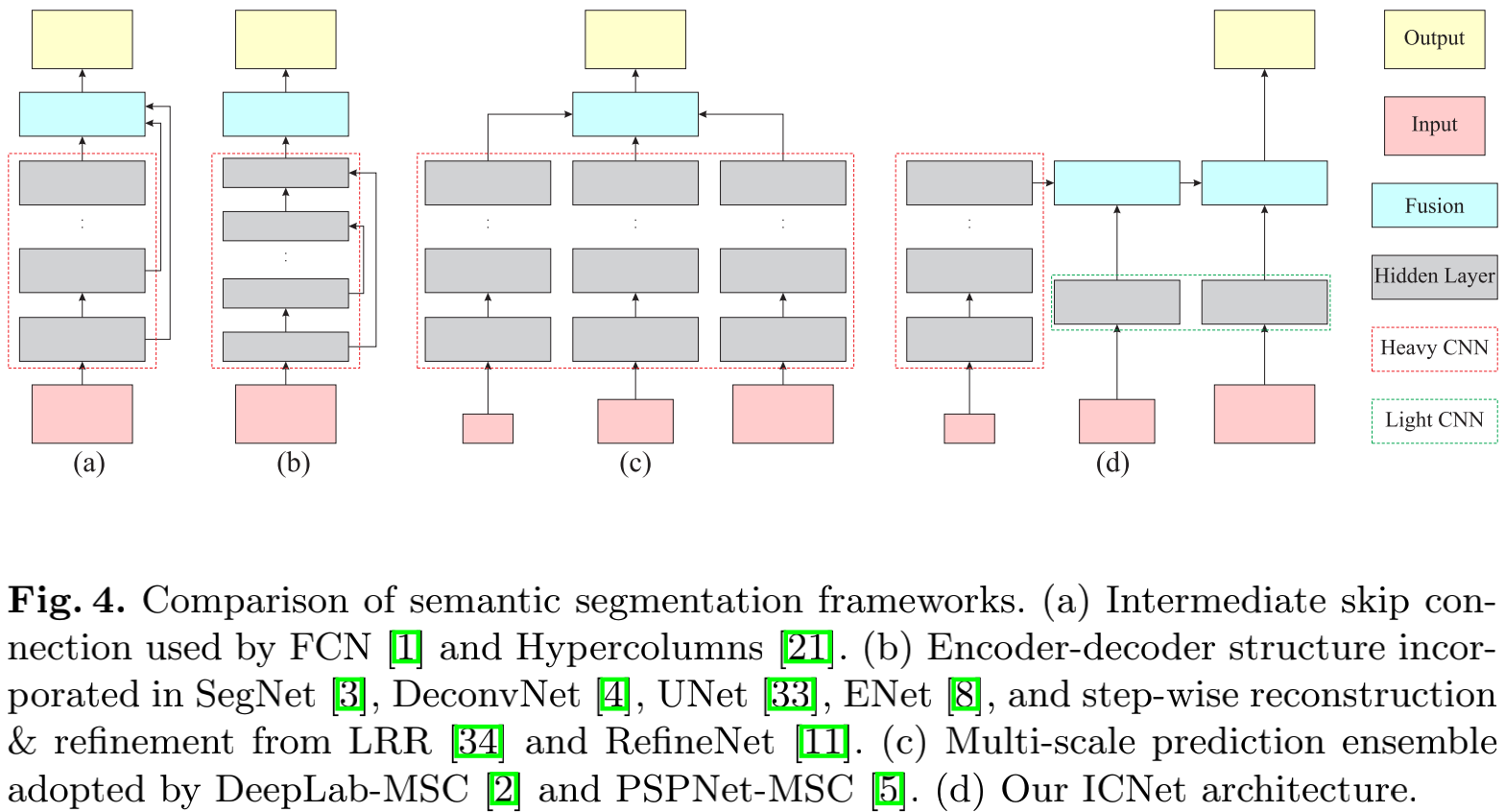
现在对ICNet与现有架构做些比较，经典的架构如上图(a),(b),(c)所示，ICNet如(d)所示。(a)的典型模型为FCN，(b)的典型模型有UNet,SegNet，(c)的典型模型有Deeplab和PSPNet。传统架构都非常的庞大，同时喂入的图片分辨率也很大。而在ICNet中，只有低分辨率的图片($\frac{1}{4}$大小的图片)喂入了大型网络中，这大大减少了计算量，高精度的原图则只喂入了轻量级的网络中用来帮助恢复图像边缘细节信息。得益于这样新提出的级联型的结构设计，ICNet有很高的实时性。

实验

作者分别在Cityscapes,CamVid,COCO-Stuff数据集上进行了实验，具体实验数据可以见原论文。可以发现它在精度和实时性之间取得了比较好的平衡，精度并没有比大型网络下降太多。速度只比ENet要慢上一些，但是ENet的精度则要比之差上很多。

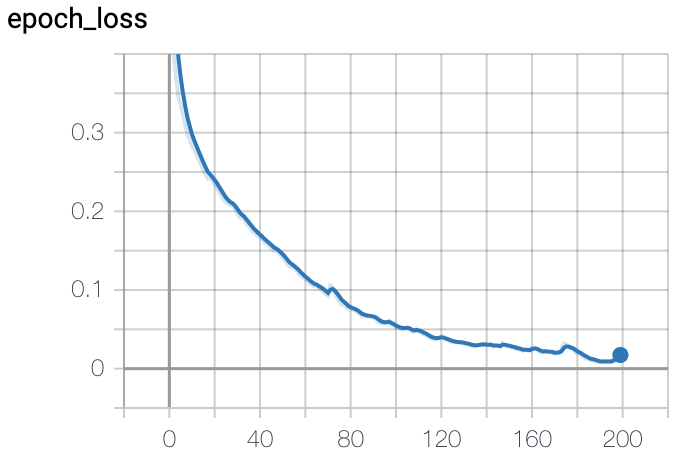
我的实验

本次实验是使用tensorflow2在google cola环境下，分配的GPU是Tesla P100。尝试了两个不同的版本，一个是不带辅助loss的，直接用最后输出层loss进行优化，发现结果竟然要好一点（不知道我的带辅助loss的写法是否正确）。

同时低分辨率图中使用的PSPNet为了简便只是用了VGG16，中分辨率图也是用VGG16下采样并且与低分辨率VGG16共享权重。

不带辅助loss

加载VGG16

base_model = keras.applications.VGG16(include_top=False)
base_model.summary()
layer = base_model.get_layer("block3_pool").output
down_stack = keras.Model(inputs=base_model.input, outputs=layer)

PSPNet中的PPM模块

def PPM(x,f):
  x_1 = AveragePooling2D((10,10))(x)
  x_2 = AveragePooling2D((5,5))(x)
  x_5 = AveragePooling2D((2,2))(x)

  x_1 = Conv2D(f,(1,1))(x_1)
  x_1 = BatchNormalization()(x_1)
  x_1 = Activation('relu')(x_1)

  x_2 = Conv2D(f,(1,1))(x_2)
  x_2 = BatchNormalization()(x_2)
  x_2 = Activation('relu')(x_2)

  x_5 = Conv2D(f,(1,1))(x_5)
  x_5 = BatchNormalization()(x_5)
  x_5 = Activation('relu')(x_5)

  x_1 = UpSampling2D((10,10),interpolation='bilinear')(x_1)
  x_2 = UpSampling2D((5,5),interpolation='bilinear')(x_2)
  x_5 = UpSampling2D((2,2),interpolation='bilinear')(x_5)

  x = Concatenate()([x,x_1,x_2,x_5])
  return x

PSPNet

def PSPnet(input_shape):
  x_input = Input(input_shape)


  x = down_stack(x_input)
  x = PPM(x,128)
  x = Conv2D(256,(3,3),padding='same')(x)
  x = BatchNormalization()(x)
  x = Activation('relu')(x)

  model = keras.Model(x_input,x)
  return model

ICNet

def ICNet(input_shape,n_class):
  x_input = Input(input_shape)

  #1/4图片
  x_4 = Lambda(lambda x:tf.image.resize(x,size=(int(x.shape[1])//4, int(x.shape[2])//4)))(x_input)
  x_4 = PSPnet((80,80,3))(x_4)

  #1/2图片
  x_2 = Lambda(lambda x:tf.image.resize(x,size=(int(x.shape[1])//2, int(x.shape[2])//2)))(x_input)
  x_2 = down_stack(x_2)

  x_4 = UpSampling2D((2,2),interpolation='bilinear')(x_4)

  #1/4图片的分支模型，用来计算辅助loss
  x_4_ = Conv2D(n_class,(1,1),activation='softmax')(x_4)
  model_16 = keras.Model(x_input,x_4_)

  x_4 = Conv2D(256,(3,3),dilation_rate=2,padding='same')(x_4)
  x_4 = BatchNormalization()(x_4)
  x_2 = Conv2D(256,(1,1),padding='same',use_bias=False)(x_2)
  x_2 = BatchNormalization()(x_2)
  x_2 = Add()([x_2,x_4])
  x_2 = Activation('relu')(x_2)

  x = Conv2D(64,(3,3),padding='same')(x_input)
  x = Conv2D(64,(3,3),padding='same')(x)
  x = MaxPool2D(padding='same')(x)
  x = Conv2D(128,(3,3),padding='same')(x)
  x = Conv2D(128,(3,3),padding='same')(x)
  x = MaxPool2D(padding='same')(x)
  x = Conv2D(256,(3,3),padding='same')(x)
  x = Conv2D(256,(3,3),padding='same')(x)
  x = Conv2D(256,(3,3),padding='same')(x)
  x = MaxPool2D(padding='same')(x)

  x_2 = UpSampling2D((2,2),interpolation='bilinear')(x_2)

  #1/2图片的分支模型，用来计算辅助loss
  x_2_ = Conv2D(n_class,(1,1),activation='softmax')(x_2)
  model_8 = keras.Model(x_input,x_2_)

  x_2 = Conv2D(256,(3,3),dilation_rate=2,padding='same')(x_2)
  x_2 = BatchNormalization()(x_2)
  x = Conv2D(256,(1,1),padding='same',use_bias=False)(x)
  x = BatchNormalization()(x)
  x = Add()([x,x_2])
  x = Activation('relu')(x)

  x = UpSampling2D((2,2),interpolation='bilinear')(x)
  x = Conv2D(256,(3,3),padding='same')(x)
  x = BatchNormalization()(x)
  x = Activation('relu')(x)
  x_ = Conv2D(n_class,(1,1),activation='softmax')(x)
  model_4 = keras.Model(x_input,x_)

  # x = UpSampling2D((4,4),interpolation='bilinear')(x)
  # x = Conv2D(n_class,(1,1))(x)
  # x = Activation('softmax')(x)

  # model = keras.Model(x_input,x)
  return model_4,model_8,model_16

训练

model_4,model_8,model_16 = ICNet((320,320,3),17)
model_4.compile(optimizer = keras.optimizers.Adam(learning_rate=0.0005),
                 loss = keras.losses.CategoricalCrossentropy(),
                 metrics = ['accuracy'])
model_4.fit(train_x,train_y_4_oh,epochs = 200,batch_size = 16,callbacks=[tensorboard_callback])

可以看到只对最后的输出模型进行训练，没有训练其它分支模型，标签数据集train_y_4_oh是对原始图片标签进行插值缩小$\frac{1}{4}$得到的。最终模型会输出$\frac{1}{4}$原图大小的预测图片，再进行4倍上采样就可得到原图大小，这样的方法速度非常快，但是会带来一些精度的缺失，也可以直接在原图大小的标签集上进行训练，速度会稍慢但是精度比较高。

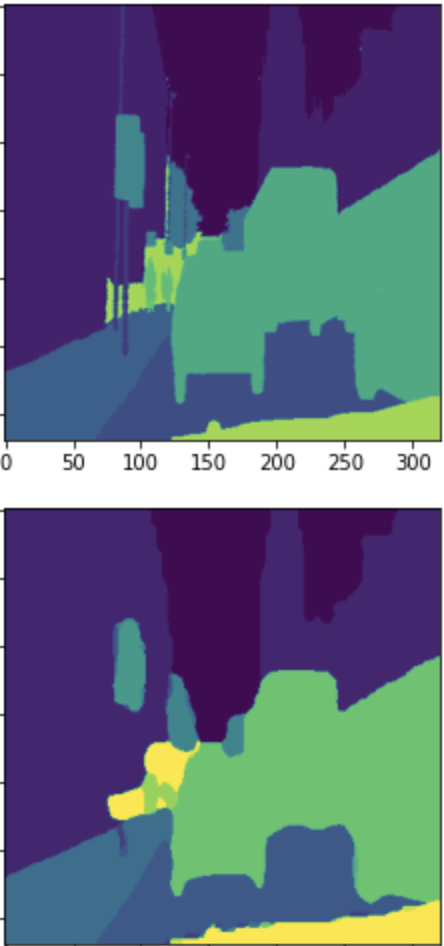
结果图

本实验使用的是输出$\frac{1}{4}$大小的预测图再进行4倍上采样，在边缘上显得不那么完美比较毛糙，但是物体位置和大概轮廓都是准确的。如果想要更精准的预测图可以直接再原图大小标签集上训练。

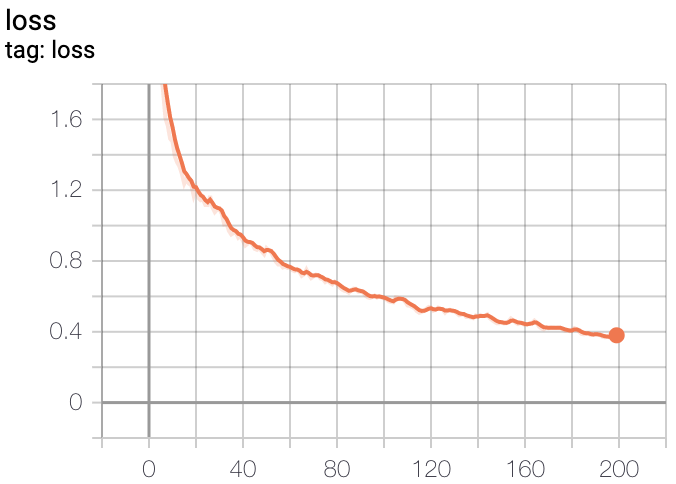
带辅助loss

模型的搭建部分与前面一样，包括ICNet部分，主要在训练部分不再使用keras中Model的fit方法，而是要使用tensorflow2的eager模式。

训练

1 2	cross_entropy = tf.losses.CategoricalCrossentropy() optimizer = tf.keras.optimizers.Adam(learning_rate=0.0005)

@tf.function()
def train_step(img,labels_16,labels_8,labels_4,labels):
  l1 = 0.4
  l2 = 0.4
  l3 = 1.
  with tf.GradientTape() as tape:
    images_16 = model_16(img)
    loss_16 = cross_entropy(labels_16,images_16)
    images_8 = model_8(img)
    loss_8 = cross_entropy(labels_8,images_8)
    images_4 = model_4(img)
    loss_4 = cross_entropy(labels_4,images_4)
    
    total_loss = l3*loss_4+l2*loss_8+l1*loss_16

  gradients = tape.gradient(total_loss, model_4.trainable_variables)

  optimizer.apply_gradients(zip(gradients, model_4.trainable_variables))
  return total_loss

def train(epochs, batch_size=16):
  m = train_x.shape[0]
  step_per_epoch = m // batch_size
  for epoch in range(epochs):
    tloss = 0
    for i in range(step_per_epoch):
      tloss += train_step(train_x[i*batch_size:(i+1)*batch_size],train_y_16_oh[i*batch_size:(i+1)*batch_size],train_y_8_oh[i*batch_size:(i+1)*batch_size],train_y_4_oh[i*batch_size:(i+1)*batch_size],train_y_oh[i*batch_size:(i+1)*batch_size])
    tloss += train_step(train_x[(i+1)*batch_size:],train_y_16_oh[(i+1)*batch_size:],train_y_8_oh[(i+1)*batch_size:],train_y_4_oh[(i+1)*batch_size:],train_y_oh[(i+1)*batch_size:])
    mloss = tloss / (step_per_epoch+1)
    with train_summary_writer.as_default():
      tf.summary.scalar('loss', mloss, step=epoch)
    display.clear_output(wait=True)
    print('第'+str(epoch+1)+'轮训练')
    print('loss:'+str(mloss))
    r = model_4(np.expand_dims(train_x[0],axis = 0))
    r = UpSampling2D((4,4),interpolation='bilinear')(r)
    plt.imshow(train_y[0])
    plt.show()
    plt.imshow(create_mask(r)[:,:,0])
    plt.show()